ABC189-C Mandarin Orange 解説（Dancing Links 編）

$O(N \log N)$ で解きます。$O(N)$ はこちら

問題

問題ページ

概要

$$ \max _ {1 \leq l \leq r \leq n} \left\lbrace (r - l + 1) \cdot \min _ {l \leq i \leq r} a _ i \right\rbrace $$

解法

以下では、載っているミカンが多い皿を「大きい皿」、少ないものを「小さい皿」、ミカンを取る皿の範囲を「収穫範囲」と表現します。

「概要」では特に断りなく変形しましたが、収穫範囲を決めたらそこから取れるだけ取りたいので、最終的に一つの皿から取るミカンの個数は範囲内で最も小さい皿に一致します。 逆に一つの皿から取るミカンの個数を決めたなら、収穫範囲はできるだけ広くした方がいいです。 そこで、それぞれの皿ごとに「その皿のミカンを全て取るとした時、収穫範囲を左右どこまで広げられるか」を考えます。以下の二つの方針が考えられます。

皿が大きい順に調べる

単純に考えるために、全ての皿に載っているミカンの個数がそれぞれ違うとします。

まず一番大きい皿（ $A$ とします）を見ると、その両脇の皿（ $B, C$ とします）は $A$ よりも小さいので、収穫範囲は左右どちらにも伸ばすことができません。

Aの収穫範囲

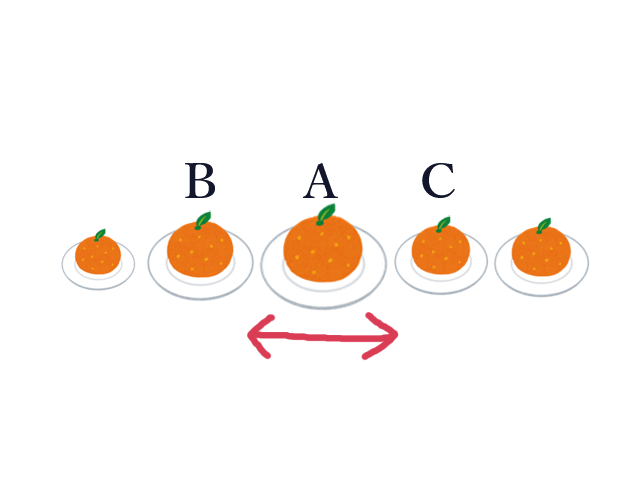
この時、逆に皿 $B$ から見ると、皿 $A$ は確実に $B$ の収穫範囲に含めることができます。よって、 $B$ を見るときには $A$ は飛ばして、 $C$ が含められるかどうかを調べればよいです。 $C$ についても同様です。 そこで、 $A$ を無かったことにして、 $B$ と $C$ を隣合わせにします。

Aを無視する

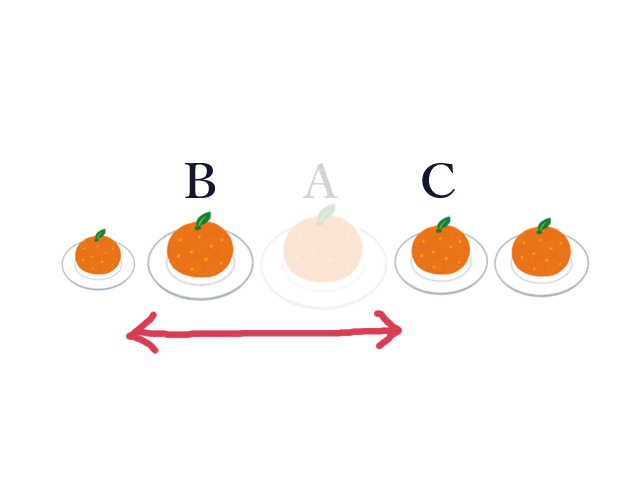
次に見る皿が $B$ だったとします。大きい順に見ているので、 $C$ は $B$ よりも小さく、収穫範囲には含められないことが分かります。 逆に $C$ から見ると、 $C$ の収穫範囲を調べる時には $A$ だけでなく $B$ もスキップしていいことが分かります。

どんどん消えていく

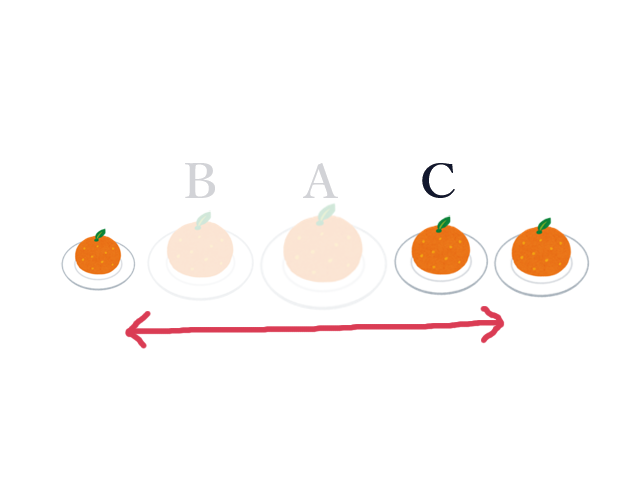
このように考えていくと、大きい順に見ている場合、

スキップできることが決まっている皿は収穫範囲に含めることができるが、その先（今隣り合っている皿）は自分より小さいので収穫範囲に含めることができない

ことが分かります。よって、皿が大きい順に

1. 両隣の皿に挟まれた範囲を収穫範囲とする
2. 皿を取り除き、両隣にあった皿を新しく隣り合わせる

という操作を繰り返すことで、全ての皿について最大の収穫範囲がわかるので、最終的な答えも求めることができます。

ところで、今は「同じ大きさの皿がない」と問題を単純化していましたが、この制約を外しても上述の考え方で答えを求めることができます。 最終的な答えを与える収穫範囲を「最適な範囲」と呼ぶことにします。この範囲は、範囲内で最小の皿 $X$ について操作を行う際に得られるもののはずです。最適な範囲の中に同じ大きさの皿が複数個含まれていたとします。これが $X$ よりも大きい場合、結局 $X$ を見ているときにはどちらも取り除かれていて、取り除かれた順番は関係ありません。 $X$ と同じ大きさの皿があった場合、それらを処理してから最後に $X$ の操作を行うことにすれば、最適な区間が得られます。さらに、同じ大きさの皿であればどれを $X$ に選んでも関係がなく、適当な順番に操作をして最後になったものを $X$ としてしまえば良いです。

よって、同じ大きさの皿が含まれている場合でも、それらについては順不同で操作を行うことができます。

この解法をコードに落とし込む際、実際に配列から削除していくのは効率が悪いです。そこで、すべての皿に対して自身の左右の皿へのポインタを持たせます。といっても、対応する皿のインデックスを持たせてポインタ代わりにすれば良いです。 ある皿について操作をするとき、左右の皿のインデックスから収穫範囲が分かります。そして皿を取り除く際には、代わりに左右の皿のポインタを付け替えてあげます。こうすることで自分自身をスキップさせることができます。

両隣のポインタをちょっといじる

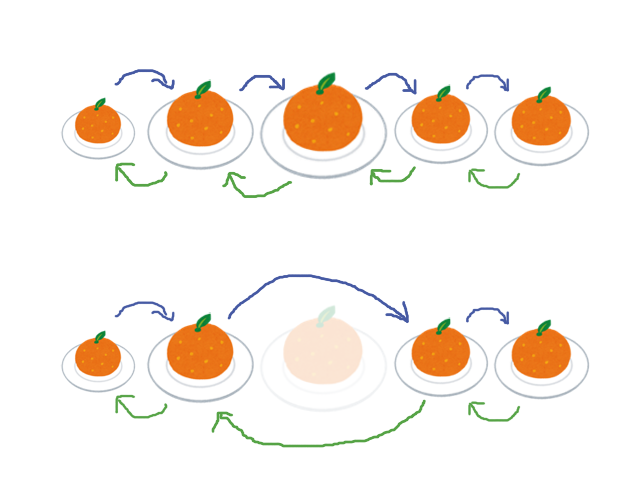
ポインタの付け替えは $O(1)$ で済むので、全体の計算量は最初のソートがボトルネックになり $O(N\log N)$ です。

実装

実装の際は両端の処理に注意しましょう。両端に大きさ $0$ の皿を番兵として置いておくと良いと思います。 以下の実装ではPythonの仕様を利用して、末尾に一つ番兵を足すことで済ませています。

n = int(input())
a = list(map(int, input().split()))
a += [0] # 番兵

left = list(range(-1, n)) # left[i]: 皿iの左隣の皿の番号
right = list(range(1, n+2))

ans = 0

# 大きい順に処理
l = list(range(n))
l.sort(key=lambda i: a[i])
l.reverse()
for i in l:
    s = right[i] - left[i] - 1 # 収穫範囲
    ans = max(ans, s * a[i])

    # 「左隣の右隣」と「右隣の左隣」を書き換える
    right[left[i]] = right[i]
    left[right[i]] = left[i]

print(ans)

提出

提出コード(Python3)