AtCoder提出ページのタブ幅を変えるスクリプト
AtCoderの提出詳細で見れるコードは、デフォルトでタブ幅が8に固定されています。

作りました。
AtCoder Tab 4matter
2021/05/03 追記
TamperMonkey から Stylus に移行しました。
AtCoder Tab 4matter

嬉しい~~
yukicoder No.119 旅行のツアーの問題 解説
余談が本編
問題
リンクはこちら
概要
$N$ 個の国があり、それぞれの国 $i \; (0 \leq i < N)$ に対して以下の行動のうち一つを選ぶ。
- 選択 $p$ : ツアー旅行に行く。利得 $b_i$
- 選択 $q$ : 個人旅行に行く。利得 $c_i$
- 選択 $r$ : 行かない。利得 $0$
ただし、いくつかの国のペア $i, j$ に対して「国 $i$ のツアー旅行に行くならば、国 $j$ の個人旅行に行ってはならない」という形の制約が課される。得られる最大の利得を求めよ。
解法
パッと見た感じだとProject Selection Plobrem(PSP、「燃やす埋める」などとも呼ばれています)を使って解けそうだけど、取りうる状態が三つあるので少し工夫が必要です。ここでは二種類の方針を紹介します。
注意 :「燃やす埋める」という名前を嫌う人がいるので記事中ではPSPと表現していますが、この記事でやっていることは紛れもなく「燃やす埋める」です(考え方が少し違うらしい)。本物のPSPについてはこちらの記事で解説されています。
1. 辺の切断
まず多くの人が解説している方針を紹介します。
一般的にはPSPは頂点の割り振りに関する問題として捉えられますが、ここでは「辺をいくつか選んで切断する」という、本来の最小カット問題に近い形式で問題を解釈してみます。
各 $i$ について、無条件に利得 $b_i + c_i$ が得られるとした上で、始点 $\mathrm{S}$ から頂点 $i$ にコスト $b_i$ 、頂点 $i$ から終点 $\mathrm{T}$ にコスト $c_i$ の辺を張ります。すると、 $\mathrm{S}$ から $\mathrm{T}$ を到達不可能にするためには、少なくともこのどちらかの辺は切らなくてはなりません。最終的に得られる利得に注目すると、前者を切ることが $q_i$ 、後者を切ることが $p_i$ 、そしてどちらも切ることが $r_i$ に相当していることがわかります。

次に禁止制約「 $p_i \to \lnot q_j$ 」を考えると、これは $p_i$ と $q_j$ が同時に選ばれたときに $\mathrm{S}$ から $\mathrm{T}$ への経路が残っているようにすればいいので、 $i$ から $j$ にコスト $\infty$ の辺を張ることで表現できます。
しかし、これだとサンプル3のようなケースで失敗してしまいます。

禁止制約の辺が連鎖して、本来許されるはずの選択までブロックしてしまっています。そこで、制約の連鎖が起こらないように、各頂点を2つずつに分割して以下のように辺を張り直してみます。

$i_1$ と $i_2$ は元々同じ頂点を表しているので、これらは分断されないようにコスト $\infty$ の辺で繋いでおきましょう。こうすることで、禁止制約は上流から下流への一方通行になり、連鎖することを防げます。
このグラフで始点から終点への最小カット(=最大流)を求めればいいです。最小カットのコストを $K$ とすると、最終的な答えは $\sum_{i} (b_i+c_i) - K$ となります。
let u = |i| { 2 * i }; // i_1 let v = |i| { 2 * i + 1 }; // i_2 let source = u(n); let sink = v(n); let mut ans = 0; let mut din = Dinic::new(); for &(i, j) in &cl { // 禁止制約 din.add_edge(u(i), v(j), INF); } for (i, &(b, c)) in plans.iter().enumerate() { // 各選択の報酬 ans += b + c; din.add_edge(source, u(i), b); din.add_edge(u(i), v(i), INF); din.add_edge(v(i), sink, c); } ans -= din.max_flow(source, sink).0;
2. 頂点の分配
続いて、一般的なPSP同様、頂点を始点側と終点側に割り振る問題として捉える方針で解いてみます。 ソースを $\text{True}(\top)$ 、シンクを $\text{False}(⊥)$ として、頂点を割り振っていきます。
以下の二頂点を用意します。
- $u_i$ : 国 $i$ のツアー旅行に行くか、国 $i$ を訪れない($p_i \lor r_i$)
- $v_i$ : 国 $i$ のツアー旅行に行く($p_i$)
こうすることで、$u_i$ と $v_i$ の真偽と行動選択が以下の通りに対応します。
- $u_i \land v_i = (p_i \lor r_i) \land p_i = p_i$
- $u_i \land \lnot v_i = (p_i \lor r_i) \land \lnot p_i = r_i$
- $\lnot u_i \land v_i = \lnot (p_i \lor r_i) \land p_i = ⊥$
- $\lnot u_i \land \lnot v_i = \lnot (p_i \lor r_i) \land \lnot p_i = \lnot p_i \land \lnot r_i = q_i$
よって、 $u_i, v_i$ の割り当てに応じたコストは以下の表の通りとなります。
$$ \begin{array}{c|cc} & u_i & \lnot u_i \\ \hline v_i & -b_i & \infty \\ \lnot v_i & 0 & -c_i \\ \end{array} $$
無条件で $b_i + c_i$ の利得が得られることにすると、以下のようにコストは全て正の値となります。
$$ \begin{array}{c|cc} & u_i & \lnot u_i \\ \hline v_i & c_i & \infty \\ \lnot v_i & b_i + c_i & b_i \\ \end{array} $$
ちゃんと劣モジュラになってるので、これは通常の2変数に関するコストとして表現可能です。例えばこんな感じ。

さらに、追加制約「$p_i \to \lnot q_j$」は、$v_i \to u_i$ を用いることで
$$ \begin{aligned} p_i \to \lnot q_j & \Leftrightarrow (u_i \land v_i) \to \lnot (\lnot u_j \land \lnot v_j) \\ & \Leftrightarrow v_i \to (u_j \lor v_j) \\ & \Leftrightarrow v_i \to u_j \end{aligned} $$
と言い換えることができるので、以下のように辺を張ればいいです。

これで始点から終点まで流せばOKです。最終的な答えは $\sum_{i} (b_i+c_i) - K$ です。
let u = |i| { 2 * i }; let v = |i| { 2 * i + 1 }; let source = u(n); let sink = v(n); let mut ans = 0; let mut din = Dinic::new(); for &(i, j) in &cl { // 禁止制約 din.add_edge(v(i), u(j), INF); } for (i, &(b, c)) in plans.iter().enumerate() { // 各選択の報酬 ans += b + c; din.add_edge(v(i), u(i), INF); din.add_edge(source, u(i), b); din.add_edge(u(i), v(i), b + c); din.add_edge(v(i), sink, c); } ans -= din.max_flow(source, sink).0;
提出
余談
初見で解いていたとき、「三種類の値を取るときは、各要素に対して二つの頂点を用意していい感じに包含関係を入れるといい」という話を何となく聞いたことがあったので、二種類の命題
- $x_i$ : 国 $i$ を訪れる($p_i \lor q_i$)
- $y_i$ : 国 $i$ のツアー旅行に行く($p_i$)
を頂点として作ることにしたのですが、間違いでした。$p$ と $q$ には「国を訪れる」という分かりやすい共通項がある上、元問題文では禁止制約があたかも「国を訪れる」という括りがあるかのように表現されていたために纒めたくなってしまいましたが、実際には完全に別の事象として捉えるべきでした(というか実際にそう)。まんまと罠にかかりました。
$x, y$ の真偽もうまく $p, q, r$ に対応して、コストも劣モジュラになりますが、禁止制約が「 $y_i \to \lnot x_j \lor y_j$ 」となってしまい、グラフで表現することができません。
包含関係をどのように設定すればうまくいきそうか、を判断する材料として、二種類の方針を紹介します。
1. 包含関係のある条件の一般的な表現
こちらの記事の後半で紹介されている考え方です。 $k$ 状態を取りうる変数を、今回作ったグラフのように
- $a_1 = s_1$
- $a_2 = s_1 \lor s_2$
- $\vdots$
- $a_{k - 1} = s_1 \lor s_2 \lor \cdots \lor s _ { k - 1 }$
という $k - 1$ 個の頂点 $a_1, a_2, ..., a _ { k - 1 } $ で表現すると、グラフの形は以下のようになります。

$a_k = s_1 \lor s_2 \lor \cdots \lor s _ k$ は必ず $\top$ になるので、頂点を用意する必要はありません。また、 $a _ {i - 1} \to a _ i$ が成り立つので、 $a _ {i-1} \land \lnot a _ i$ という状態に無限のコストがかかるように逆向きの辺を張っています。
まずは一つの変数のみに着目します。 1変数関数は必ず劣モジュラであるので、適切に辺コストを割り振りさえすればこのグラフによって各 $s _ i$ のコストは必ず表現できます。 例えば $s_i$ を選んだ際のコストを $\theta(s _ i)$ として、以下のように対応していたとします。
$$ \begin{array}{c|cccc} i & 1 & 2 & 3 & 4 \\ \hline \theta(s _ i) & -5 & 6 & 2 & -8 \\ \end{array} $$
このとき、任意の定数 $w$ を用いて、無条件に $w$ の報酬がもらえるとした上で、以下のように辺のコストを定めることで $\theta$ が表現できます。

$a _ i \land \lnot a _ { i - 1 } \to s _ i $ が成り立つので、$ a _ i , a _ { i - 1 } $ 間の辺を切るときには 「その選択肢のコスト $\theta(s _ i)+$ 無条件にもらえてしまった報酬 $w$」のコストがかかるようにします。 $w$ はどの辺を選んでも打ち消される値なのでなんでもよく、適切な値をとることで負辺をなくすことができます。
次に、全ての変数 $i$ に対してこれらの頂点 $a ^ { i } _ {d} \;( 1 \leq d < k ) $ を用意したあと、ある頂点から別の頂点に張った辺がどのような意味を持つのかを考えてみます。 $a ^ { i } _ { n }$ から $a ^ { j } _ { m }$ へとコスト $c$ の辺を張ってみます。

このコストがかかるのは $a ^ { i } _ { n } \land \lnot a ^ { j } _ { m }$ のときです。つまりこの辺は「 $i$ が $s_1, s_2, \ldots, s _ n$ のどれかであるとき、$j$ が $s_1, s_2, \ldots, s _ m $ のどれかでないならコスト $c$ がかかる」と翻訳できます。 先程挙げたブログの言葉を借りてこれを一般化すると、包含関係のある集合 $A_1 \subset A_2 \subset A_3 \subset \cdots$ に変数 $v_1, v_2, v_3, \ldots$ を配置していくとき、「 $v _ i \in A _ n$ かつ $v _ j \not \in A _ m $ ならコスト $c \;(> 0)$ がかかる」という条件を表現できます。
これを踏まえて元の問題の禁止制約「$p _ i \to \lnot q _ j$」を「$p _ i \to p _ j \lor r _ j$」と解釈すれば、 $p, p \lor r$ という括りを作ることで上手くいきそうだ、とあたりをつけることができるかと思います。
2. Monge行列への意識
本問題では、禁止制約に関するコスト行列は以下のようになっています。
$$ \begin{array}{c|ccc} & p_i & q_i & r_i \\ \hline p_j & 0 & 0 & 0 \\ q_j & \infty & 0 & 0 \\ r_j & 0 & 0 & 0 \\ \end{array} $$
これがMongeになるよう選択肢を並び替えます。
$$ \begin{array}{c|ccc} & p_i & r_i & q_i \\ \hline p_j & 0 & 0 & 0 \\ r_j & 0 & 0 & 0 \\ q_j & \infty & 0 & 0 \\ \end{array} $$
するとここをこうまとめたくなります。(?)
$$ \begin{array}{c|c:cc} & p_i & r_i & q_i \\ \hline p_j & 0 & 0 & 0 \\ r_j & 0 & 0 & 0 \\ \hdashline q_j & \infty & 0 & 0 \\ \end{array} $$
「 $p_i \land \lnot q_j$ 」 $=$ 「 $p_i \land \lnot (p_j \lor r_j)$ 」の場合にコストをかけたいので、 $p, p \lor r$ という二種類の頂点があればグラフで表現出来そうだな、という風に思える、らしいです。また、このようにすると $q, q \lor r$ という二種類の頂点を作ってもなんとかなりそうに思えますね(実際なんとかなる)。
正直この方法にどのくらい汎用性があるのかは分かりません。ただ、これに限らず、グラフ表現をする上でコストが劣モジュラであることが必要だということを常に念頭におきながら問題を整理することで、なんとなく見通しを立てやすくなるのかもしれません。
参考記事
ABC189-C Mandarin Orange 解説(stack 活用編)
$O(N)$ で解きます。$O(N \log N)$ はこちら
問題
概要
$$ \max _ {1 \leq l \leq r \leq n} \left\lbrace (r - l + 1) \cdot \min _ {l \leq i \leq r} a _ i \right\rbrace $$
解法
前回の続きです。今回は皿の大きさ順ではなく、シンプルに左から見ていくことにします。
再び「その皿のミカンを全て取るとした時、収穫範囲を左右どこまで広げられるか」を考えます。 ここで、左に伸ばすことと右に伸ばすことはお互いに影響しないので、まず「どこまで左に伸ばせるか」を考えます。
どこまで伸ばせるかというと、「自分より小さな皿のうち最も近いもの」(境界)の一個手前までです。全ての皿について、境界を順番に計算していきます。 ある皿の左側がこのようになっていたとします。

この時、次に見る皿の大きさに関わらず、 $11$ の皿は絶対に境界にはなりません。右隣にある $2$ の皿の方が小さく、しかも必ず次に見る皿に近くなってしまうからです。同様に、 $4, 19$ の皿も境界にはなりません。このように考えると、境界の候補は以下のように単調に増加する数列として表されます。

単調なので、二分探索によって境界の位置を求めることができます。
その後、この列に今見た皿が追加されますが、新たに $9, 80$ の皿が絶対に境界にならなくなりました。よって、この皿も削除してしまいます。

この時、左側で残っている皿が単調増加であることから、削除するべき大きい皿は常に末尾に固まっているはずなので、末尾が自分より大きい限り削除を続ければよいです。 削除が終わったとき、末尾にあるものは先程二分探索で見つけた境界のはずです。ということは、先に削除の操作を行ってしまえば二分探索をしなくても境界を求めることができるということです。
よって、左側にある皿を蓄えるstackを用意して、
- 自分より大きな皿を削除(末尾からの
popを繰り返す) - 境界を記録して、自分を追加
を繰り返すことで、全ての皿について境界(収穫範囲の左端)を求めることができます。
push、popの計算量は $O(1)$ であり、全ての皿は高々一度づつしか追加・削除されないので、計算量は合計で $O(N)$ です。
同様にこれを右側から行えば、それぞれの収穫範囲の右端も求めることができます。よって全ての皿に対して最大の収穫範囲が求まるので、あとはそれらのうち答えが最大になるものを計算すれば良いです。 計算量は全体で $O(N)$ です。
実装
境界を探すのを簡単にするため、stackには皿の大きさではなくindexを入れています。 また、stackが空になった時の処理を単純化するため予め番兵を入れています。
n = int(input()) a = list(map(int, input().split())) a += [0] # 番兵 left = [0] * n # left[i]: 皿iの左の境界 right = [0] * n # 左から見る st = [-1] # 番兵 for i in range(n): while a[st[-1]] >= a[i]: st.pop() left[i] = st[-1] st.append(i) # 右から st = [n] # 番兵 for i in range(n-1, -1, -1): while a[st[-1]] >= a[i]: st.pop() right[i] = st[-1] st.append(i) ans = max(a[i] * (right[i] - left[i] - 1) for i in range(n)) print(ans)
提出
提出コード(Python3)
ABC189-C Mandarin Orange 解説(Dancing Links 編)
$O(N \log N)$ で解きます。$O(N)$ はこちら
問題
概要
$$ \max _ {1 \leq l \leq r \leq n} \left\lbrace (r - l + 1) \cdot \min _ {l \leq i \leq r} a _ i \right\rbrace $$
解法
以下では、載っているミカンが多い皿を「大きい皿」、少ないものを「小さい皿」、ミカンを取る皿の範囲を「収穫範囲」と表現します。
「概要」では特に断りなく変形しましたが、収穫範囲を決めたらそこから取れるだけ取りたいので、最終的に一つの皿から取るミカンの個数は範囲内で最も小さい皿に一致します。 逆に一つの皿から取るミカンの個数を決めたなら、収穫範囲はできるだけ広くした方がいいです。 そこで、それぞれの皿ごとに「その皿のミカンを全て取るとした時、収穫範囲を左右どこまで広げられるか」を考えます。以下の二つの方針が考えられます。
皿が大きい順に調べる
単純に考えるために、全ての皿に載っているミカンの個数がそれぞれ違うとします。
まず一番大きい皿( $A$ とします)を見ると、その両脇の皿( $B, C$ とします)は $A$ よりも小さいので、収穫範囲は左右どちらにも伸ばすことができません。
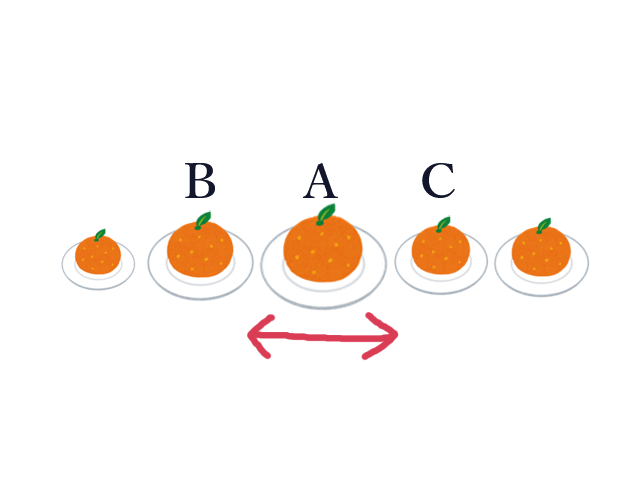
この時、逆に皿 $B$ から見ると、皿 $A$ は確実に $B$ の収穫範囲に含めることができます。よって、 $B$ を見るときには $A$ は飛ばして、 $C$ が含められるかどうかを調べればよいです。 $C$ についても同様です。 そこで、 $A$ を無かったことにして、 $B$ と $C$ を隣合わせにします。
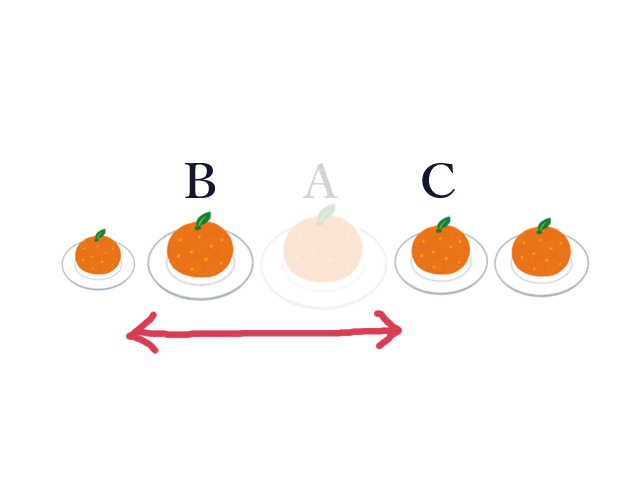
次に見る皿が $B$ だったとします。大きい順に見ているので、 $C$ は $B$ よりも小さく、収穫範囲には含められないことが分かります。 逆に $C$ から見ると、 $C$ の収穫範囲を調べる時には $A$ だけでなく $B$ もスキップしていいことが分かります。
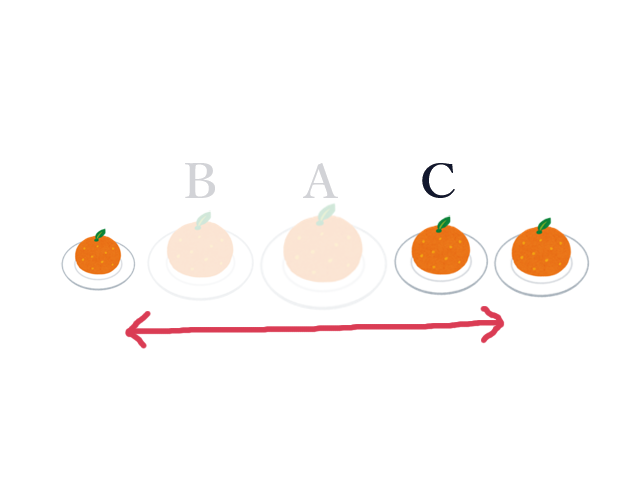
このように考えていくと、大きい順に見ている場合、
スキップできることが決まっている皿は収穫範囲に含めることができるが、その先(今隣り合っている皿)は自分より小さいので収穫範囲に含めることができない
ことが分かります。よって、皿が大きい順に
- 両隣の皿に挟まれた範囲を収穫範囲とする
- 皿を取り除き、両隣にあった皿を新しく隣り合わせる
という操作を繰り返すことで、全ての皿について最大の収穫範囲がわかるので、最終的な答えも求めることができます。
ところで、今は「同じ大きさの皿がない」と問題を単純化していましたが、この制約を外しても上述の考え方で答えを求めることができます。 最終的な答えを与える収穫範囲を「最適な範囲」と呼ぶことにします。この範囲は、範囲内で最小の皿 $X$ について操作を行う際に得られるもののはずです。最適な範囲の中に同じ大きさの皿が複数個含まれていたとします。これが $X$ よりも大きい場合、結局 $X$ を見ているときにはどちらも取り除かれていて、取り除かれた順番は関係ありません。 $X$ と同じ大きさの皿があった場合、それらを処理してから最後に $X$ の操作を行うことにすれば、最適な区間が得られます。さらに、同じ大きさの皿であればどれを $X$ に選んでも関係がなく、適当な順番に操作をして最後になったものを $X$ としてしまえば良いです。
よって、同じ大きさの皿が含まれている場合でも、それらについては順不同で操作を行うことができます。
この解法をコードに落とし込む際、実際に配列から削除していくのは効率が悪いです。そこで、すべての皿に対して自身の左右の皿へのポインタを持たせます。といっても、対応する皿のインデックスを持たせてポインタ代わりにすれば良いです。 ある皿について操作をするとき、左右の皿のインデックスから収穫範囲が分かります。そして皿を取り除く際には、代わりに左右の皿のポインタを付け替えてあげます。こうすることで自分自身をスキップさせることができます。
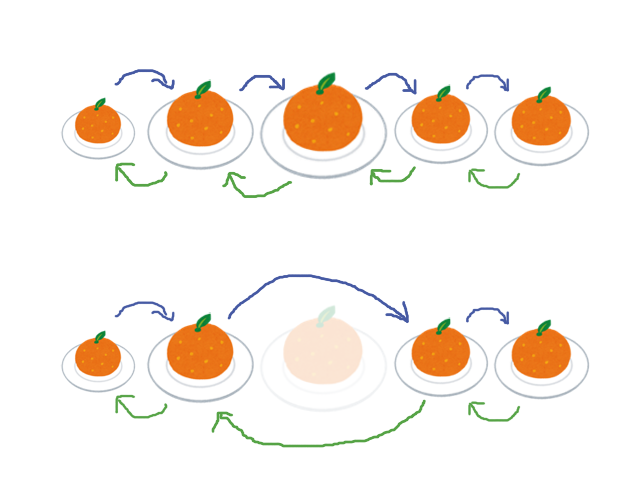
ポインタの付け替えは $O(1)$ で済むので、全体の計算量は最初のソートがボトルネックになり $O(N\log N)$ です。
実装
実装の際は両端の処理に注意しましょう。両端に大きさ $0$ の皿を番兵として置いておくと良いと思います。 以下の実装ではPythonの仕様を利用して、末尾に一つ番兵を足すことで済ませています。
n = int(input()) a = list(map(int, input().split())) a += [0] # 番兵 left = list(range(-1, n)) # left[i]: 皿iの左隣の皿の番号 right = list(range(1, n+2)) ans = 0 # 大きい順に処理 l = list(range(n)) l.sort(key=lambda i: a[i]) l.reverse() for i in l: s = right[i] - left[i] - 1 # 収穫範囲 ans = max(ans, s * a[i]) # 「左隣の右隣」と「右隣の左隣」を書き換える right[left[i]] = right[i] left[right[i]] = left[i] print(ans)
提出
提出コード(Python3)
ABC142-F Pure 解説
$O(N+M)$ で解きます。
問題
リンクはこちら
概要
$N$ 頂点 $M $ 辺の有向グラフが与えられる。極小のサイクルを一つ見つけよ。
解法
問題文に書かれている条件は「概要」のように言い換えることができます。editorialでは
- 最小のサイクルを見つける
- サイクルを一つ見つけ、どんどん小さくしていく
の二通りの方法で解いており、どちらも計算量は $O(N(N + M))$ です。
このうち後者の方法は
- サイクルを一つ見つける
- ショートカットができる限り、より小さなサイクルに更新していく
の二つのステップからなっています。この解法をベースに進めていきます。
サイクルを一つ見つける
このパートは特に工夫は要りません。 「有向グラフ サイクル 検出」などで検索するとたくさん出てくるので調べてみてください。 深さ優先探索を行うだけではありますが、非再帰で実装するのはちょっとだけ大変です。 計算量は $O(N + M)$ です。
小さなサイクルに更新していく
準備として、
$$ \begin{aligned} \mathit{used}[v] &= \begin{cases} \mathrm{true} & \text{(頂点 $v$ がサイクルに使われている)} \\ \mathrm{false} & \text{(使われていない)} \end{cases} \\ \mathit{next}[v] &= \text{サイクル上で $v$ の次の頂点} \end{aligned} $$
であるような配列 $\mathit{used}, \mathit{next}$ を作っておきます。サイクルに使われていない頂点は $\mathit{next}$ に何が入っていてもいいこととします。サイクルの長さは高々 $N$ なので、これらの配列は $O(N)$ で計算可能です。
準備ができたら、辺を順番に見ていきます。辺 $uv$ について $\mathit{used}[u] = \mathrm{true}, \mathit{used}[v] = \mathrm{true}, \mathit{next}[u] \neq v$ であるような時は、下図のような状況です。

このように、 $u$ から $v$ への経路を辺 $uv$ に置き換えることで、より小さなサイクルを作ることができます。ここでの更新処理が重要で、 サイクル上で $u$ から $v$ の間にある頂点の $\mathit{used}$ を $\mathrm{false}$ にする という処理を行います。もちろん $\mathit{next}[u]$ の更新も忘れずに行ってください。
サイクルを縮める操作は何度か行う可能性がありますが、この方法では一度 $\mathrm{false}$ になった頂点はその後処理の対象となりません。そのため、全ての辺に対する処理は合計しても $O(N+M)$ で済みます。 一方、$v$ から $u$ へと辿ってサイクルを再構成しようとすると、サイクルの大きさが $N \to N-1 \to N-2 \to \cdots$ と変化するような場合に $O(N ^ 2)$ かかってしまいます。
また、この処理の過程でサイクルに新たな頂点が追加されることはないので、それまでショートカットに使えなかった辺が新しく使えるようになることはありません。 なので、順番を気にすることなく全ての辺を一回ずつ見るだけで、それ以上のショートカットが不可能な極小のサイクルを得ることができます。
計算量は全体で $O(N+M)$ です。
実装
N, M = map(int, input().split()) edges = [tuple(map(int, input().split())) for _ in range(M)] G = [list() for _ in range(N+1)] for (u, v) in edges: G[u].append(v) # サイクル検出 seen = [-1]*(N+1) # -1: 未到達 # 0: stack追加済み # 1: 行きがけで通過済み(cycle候補) # 2: 帰りがけで通過済み curr_path = [] stack = [] def dfs(): for i in range(1, N+1): if seen[i] == 2: continue stack.append(i) while stack: u = stack.pop() if u > 0: # 行きがけ stack.append(-u) curr_path.append(u) seen[u] = 1 for v in G[u]: if seen[v] == -1: seen[v] = 0 stack.append(v) elif seen[v] == 1: cycle = curr_path[curr_path.index(v):] return cycle else: # 帰りがけ seen[-u] = 2 curr_path.pop() return list() cycle = dfs() if not cycle: print(-1) exit() # サイクルを小さくする # 準備 used = [False] * (N+1) next = [0] * (N+1) for i in range(len(cycle)): used[cycle[i]] = True next[cycle[i-1]] = cycle[i] # ショートカットできるか確かめる for (u, v) in edges: if used[u] and used[v] and next[u] != v: w = next[u] while w != v: used[w] = False w = next[w] next[u] = v # サイクル復元 u = used.index(True) ans = [u] v = next[u] while v != u: ans.append(v) v = next[v] print(len(ans)) for x in ans: print(x)
余談
ウケますね
ABC128-C Switches 解説
$ O(M ^ 2) $ (一般の $N, M $ については $ O(NM ^ 2) $ ) で解きます。
問題
リンクはこちら
概要
$N$ 個のスイッチと $M $ 個の電球がある。$i$ 番目のスイッチ $ (1\leq i\leq N) $ は $ k _ i $ 個の電球 $s _ {i1},s _ {i2},\ldots,s _ {ik _ i}(1 \leq s _ {ij} \leq M)$ の状態を切り替える。 全ての電球を ON にするスイッチの ON / OFF の決め方は何通りか?
解法
editorial解は素朴な全探索ですが、線形代数を用いて計算量を改善します。 (大学一年生レベルの線形代数の知識が必要になります。)
$N$ 次元ベクトル $\bm{x}$ 、$N \times M $ 行列 $A$ をそれぞれ
$$ \begin{aligned} \bm{x} _ i &= \begin{cases} 1 & \text{(スイッチ $i$ が ON)} \\ 0 & \text{(OFF)} \end{cases} \\ A _ {ij} &= \begin{cases} 1 & \text{(電球 $i$ がスイッチ $j$ の影響を受ける)} \\ 0 & \text{(受けない)} \end{cases} \end{aligned} $$
と定義します。求める答えは入力で与えられる $\bm{p}$ を用いて、 $\bm{x}$ についての
\[ A\bm{x} \equiv \bm{p} \quad (\mathrm{mod}\:2) \]
の解の個数に等しいです。
この解は拡大係数行列 $(A\,|\,\bm{p})$ に掃き出し法を行うことで求めることができます。また、解の自由度を $r$ とすると $r = N - \mathrm{rank}(A\,|\,\bm{p})$ です。 つまり $r$ 個のスイッチについては ON / OFF を自由に決定することができるので、解の個数は $2 ^ r$ です。 ただし、係数行列部分が全て $0$ なのに定数項が $0$ でないような行が存在した場合は 解なし となるため注意してください。計算量は $O(NM ^ 2)$ です。
さらに、演算が $\text{mod}\:2$ 上で行われること、 $N$ がワードサイズに収まる $(\leq 32)$ ことから、 以下の実装では $A$ をビットで表現し、掃き出し法をビット演算によって行っています。
$$ \begin{array}{ccc} A = \begin{pmatrix} 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 & 0 \\ \end{pmatrix} & \longrightarrow & A = \begin{pmatrix} \mathrm{01101} _ {(2)} \\ \mathrm{00011} _ {(2)} \\ \mathrm{10010} _ {(2)} \\ \mathrm{01100} _ {(2)} \\ \mathrm{01001} _ {(2)} \\ \mathrm{11100} _ {(2)} \\ \end{pmatrix} = \begin{pmatrix} 13 \\ 3 \\ 18 \\ 12 \\ 9 \\ 28 \end{pmatrix} \end{array} $$
これにより計算量は $O(M ^ 2)$ になっています。 $N$ が大きい場合にも、Pythonの多倍長整数やC++のbitsetを用いて同様の工夫を行なうことで、定数倍を大きく改善することができます。
実装
N, M = map(int, input().split()) s = [list(map(int, input().split()))[1:] for _ in range(M)] p = list(map(int, input().split())) # 行列 A の構築 A = [0] * M for i in range(M): for x in s[i]: A[i] |= 1 << (N - x) # 拡大 for i in range(M): A[i] = A[i] << 1 | p[i] # 掃き出し法 # mod2 なので XOR でよい for i in range(M): # 最も高い bit が立っている行を探す for j in range(i+1, M): if A[i] < A[j]: A[i], A[j] = A[j], A[i] if A[i] == 0: break # 掃き出す msb = 1 << (A[i].bit_length() - 1) for j in range(M): if j == i: continue if A[j] & msb: A[j] ^= A[i] # 係数が全て0 かつ 定数項が1 の行がある <=> 解なし if 1 in A: ans = 0 else: rank = sum(x > 0 for x in A) ans = pow(2, N - rank) print(ans)
ABC187-B Gentle Pairs 解説
\(O(N \log N)\) で解きます。
問題
リンクはこちら
概要
与えられる点の集合 \(S\) の中から二点を選ぶとき、それらを結んだ直線の傾きが \(-1\) 以上 \(1\) 以下になる組み合わせはいくつあるか?
解法
editorial解は単純にすべてのペアについて調べるだけですが、ここでは他の解き方を紹介します。
まず、こういう図を想像します。

点 \(\mathrm{P}\) と結んだ時に傾きが \(-1\) 以上 \(1\) 以下になるのは灰色で塗られた範囲です。よって、 \((\mathrm{P}, \mathrm{Q})\) は条件を満たしますが、 \((\mathrm{P}, \mathrm{R})\) は満たさないことが見て取れます。
この図を左に \(45^\circ\) 回転してみます。

\(45^\circ\) 回転した座標系を新たに考えると、問題の条件は「自分より左下、または右上にある」と言い替えることができます。
よって、全ての点について自身の左下にいくつの点があるかを数えることで、全てのペアを重複なく数えることができます。 これは、 \(X\) 座標の小さい順に点を見ていき、今見ている点より \(Y\) 座標の小さな点がこれまでにいくつあったかが計算できれば良いので、 平衡二分木やFenwick Treeを使うことで \(O(N \log N)\) で解くことができます。 (「平面走査」と呼ばれるテクニックです。)
class FenwickTree: # 実装略 N = int(input()) P = [tuple(map(int, input().split())) for _ in range(N)] # 座標変換 P = [(x-y, x+y) for (x, y) in P] # 座標圧縮 def compress(p): x_set = sorted(set([x for (x, y) in p])) y_set = sorted(set([y for (x, y) in p])) x_dict = {x:i for i, x in enumerate(x_set)} y_dict = {y:i for i, y in enumerate(y_set)} return [(x_dict[x], y_dict[y]) for (x, y) in p] P = compress(P) # 平面走査 P.sort() bit = FenwickTree(N) ans = 0 for (_, y) in P: ans += bit.bitsum(y+1) bit.bitadd(y, 1) print(ans)
今回の制約ではわざわざ座標圧縮を行う必要はありませんが、負数がなくなるよう底上げする処理が必要なのでせっかくだしやることにしました。